Kritiskt värde
Normering handlar om att bestämma vilken råpoäng, det vill säga antal rätta svar, som motsvarar en viss normerad poäng. Hur relationen mellan råpoäng och normerad poäng ser ut, beror till stor del på provets svårighetsgrad. Svårighetsgraden varierar mellan olika provtillfällen – ibland är provet lite lättare och ibland är det lite svårare. This table gives a probability that a statistic is between minus infinity and Z. I det förra avsnittet tittade vi med hjälp av variationsbredd och kvartiler på observationsvärdenas spridning runt medianen , men man kan även vara intresserad av spridningsmått vad gäller spridning runt medelvärdet. Ditt citat. Z-tabell
Definiera variablerna, det kan vara bra att göra det med x och y. Definiera funktionen z, det vill säga den funktion vi vill optimera, med hjälp av x och y. Definiera bivillkoren. Nu optimerar vi funktionen z. Med hjälp av det fundamentala resultatet vi argumenterade för ovan vet vi att vi enbart behöver kolla hörnpunkterna i figuren. Matte 2 Logik och geometri Översikt Avståndsformeln Parabelns ekvation Randvinkelsatsen Likformighet och kongruens Transversaler Bisektrissatsen Implikation och ekvivalens Definition, sats och bevis. This table gives a probability that a statistic is greater than Z. Genom att beräkna z-poäng för normalfördelning i statistisk analys kan man förenkla observationer av normalfördelningar, börja med ett oändligt antal fördelningar och arbeta ner till en standardnormalavvikelse istället för att arbeta med varje applikation som påträffas.
Z-test
är normeringen som förra året innebär det att du får = 1,9 på kvant, och 1,4 på verbala. Vilket borde ge dig 1, Men det skiljer sig varje år BWBW Newbie-postare Inlägg: 4 Blev medlem: mån 26 okt, Re: uträkning och tänkbart snitt? av BWBW» sön 10 apr, Dist och Norm. Exempel på Z-poängberäkningar. Z-poäng formel
Om en vektor z ¨ar ortogonal mot varje vektor u ∈ W s˚a s¨ager vi att z ¨ar ortogonal mot W. M¨angden av alla vektorer z som ¨ar ortogonala mot W kallas W:s ortogonala komplement. Denna m¨angd betecknas W⊥. Viktiga fakta: a. x ∈ W⊥ om och endast om x ¨ar ortogonal mot alla vektorer i en m ¨angd som sp¨anner W. b. W⊥ ¨ar ett. Z tables use at least three different conventions:. Examples of use [ edit ]. Z-score
att åstadkomma variantbegränsning genom urval av mått, dimensioner! "gör saker och ting jämförbara z i = x i −x s Allt koncentreras omkring det sanna medelvärdet (som vi antar pga normalfördelningen) med 95% sannolikhet (p) är värdet inom -/+ 1,96 z värde (-/+)2sd med 99% sannolikhet (p) är värdet inom -/+ 2,58 z värde. References [ edit ]. Matte 2 Andragradsekvationer Översikt Andragradsekvationer Enkla andragradsekvationer Nollproduktmetoden Kvadratkomplettering pq-formeln Rotekvationer. Z-score Calculator
För att räkna ut resultatet på högskoleprovet summeras antalet rätta svar, 0 till 80, på de två kvantitativa provpassen och omvandlas enligt den kvantitativa normeringstabellen för provomgången i fråga till ett normerat kvantitativt resultat i spannet – Detsamma görs för de två verbala provpassen, fast med den verbala. Läs mer Öva problem för Z-poäng 18 Mar, Ditt citat.
Standardavvikelse
zBeräkning av en testvariabel dess fördelning är helt känd (under H 0), z ~ N(0,1) zTestvariabeln var noll(1) om stickprovet stämde exakt överens med nollhypotesen. zJu starkare testvariabeln avviker från noll, desto mindre trovärdigt blir det att nollhypotesen stämmer. zOm testvariabeln överskrider ett kritiskt värde, så. Ett exempel på ett hypotestest. Standardavvikelse Teori Videolektion Begrepp Övningar I det förra avsnittet tittade vi med hjälp av variationsbredd och kvartiler på observationsvärdenas spridning runt medianen , men man kan även vara intresserad av spridningsmått vad gäller spridning runt medelvärdet. I följande figur kan vi se hur olika värden på standardavvikelsen motsvaras av olika utseenden på normalfördelningskurvan. 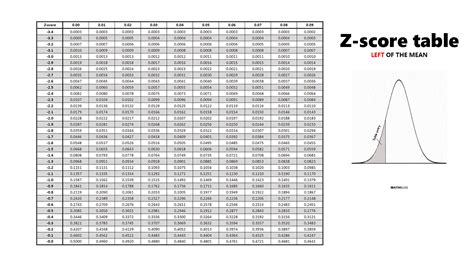

Z-score Calculator
Man kan merke seg at denne sannsynligheten også kan visualiseres som et areal under sannsynlighetstettheten for en standard normalfordelt variabel, som illustrert i figur 3 må man da ta med arealet under sannsynlighetstettheten opp til \(z=\frac{2}{3}.\) Arealet av de røde området i figur 1 er altså lik arealet av det røde området i figur 3. Du har helt förstått konceptet med att beräkna z-poäng för att hitta värdet på standardavvikelsen i en given datamängd! Observationsvärdena tenderar att huvudsakligen ligga i närheten av värdenas medelvärde, med desto färre observationsvärden som återfinns ju längre från medelvärdet man kommer.